Как написать длинный корень на клавиатуре

Способы набора на пк и ноутбуке

Часто, чтобы поставить в текст радикал или запись с ним, используются сочетания букв. Sqrt, например, означает кв. корень, а cbrt – кубический. Но писать буквенные комбинации, слова неудобно. Кроме того, они не всем понятны.

Используем таблицу символов

Удобный инструмент, работающий в различных приложениях Microsoft Office, блокноте, – таблица символов.

Вызвать ее можно несколькими способами:

• набрать в строке поиска название приложение;
• вызвать командную строку сочетанием клавиш win + r, набрать charmap.exe. Вызов осуществляется, если последовательно кликнуть «пуск», «выполнить»;
• зайти в пуск, перейти в стандартные программы, затем – служебные, выбрать искомое приложение.

Далее найти значок корня, последовательно щелкнуть выделить, копировать и вставить в нужное место.

Код символа

Простой метод вставить корень – использовать код.

Алгоритм на пк:

• включить цифровую клавиатуру, нажав NumLock;
• нажать alt и, удерживая клавишу, набрать 251 с цифрового блока.

В случае с ноутом сделать нужно так:

• внимательно посмотреть на клаву;
• найти на буквенной части цифры. Они находятся под буквами в правой части – 2 под английской K, 5 – под I, 1 – под J;
• включить функциональную клавишу, которая их активирует. Для этого кликнуть Fn и кнопку от F1 до F12 (зависит от ноутбука);
• нажать альт и 251 с активированной клавы.

При работе с документом html, в программировании используются следующие значения:

• &#8730 для квадратного корня;
• &#8731 – кубического;
• &#8732 – четвертого.

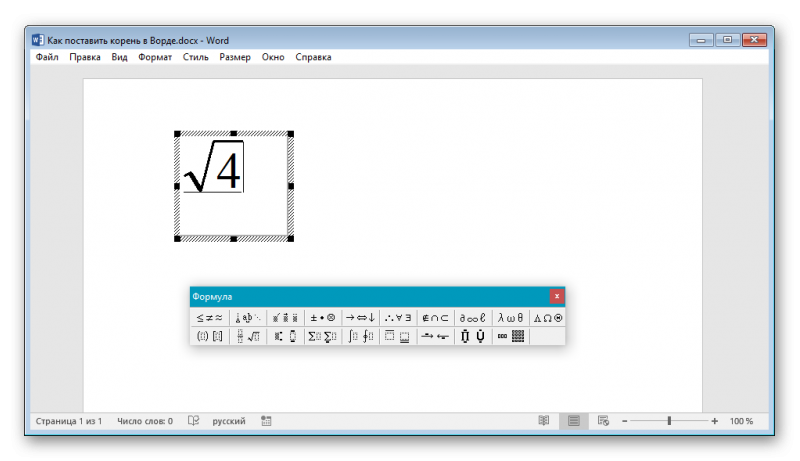
Значок корня в уравнении

В документе можно написать не просто радикал, но и целое уравнение со степенью, неизвестным составляющим.

Для этого:

• перейти во «Вставку»;
• открыть раздел формул;
• выбрать квадратное уравнение. Если нужен другой тип уравнения, вызвать функцию «вставить новую формулу»;
• заполнить значения, в том числе степень над элементом в левой его части. Она может быть третьей, пятой, седьмой – любой.

Самостоятельно уравнение с х, корнем из некоего числа записывается и через инструмент «Объект» в меню «Вставка». После нажатия на объект перейти в Microsoft equation 3.0, «Шаблоны дробей и радикалов». В открывшемся конструкторе записать уравнение.

Шестнадцатеричный код

Для включения элемента может использоваться шестнадцатеричная система Юникод.

Работает так:

• ввести кодовое значение. Квадратный корень обозначается 221A, кубический – 221B, четвертый – 221C. Буквы после цифр писать в латинской раскладке;
• одновременно выжать сочетание Alt+X.

Способы набора символа в ворде

Чтобы поставить радикал в документе word, можно использовать большинство описанных методов.

Среди них:

• скопировать элемент из другого текста, браузера, вставить;
• использовать код+alt, код шестнадцатеричной системы;
• через таблицу символов;
• с помощью встроенного редактора формул. Для этого нажимают на раздел «Вставка», выбирают «Формула», жмут на «Вставить новую формулу». Появится надпись «Место для формулы», а в верхней панели инструментов – конструктор математических знаков. Остается выбрать значок и подкоренное выражение. Можно сразу выбрать значок со степенью 2, 3, 4, 5, даже 6;
• через инструмент «Объект»;
• изобразить значок в графическом редакторе – нарисовать галочку, одну сторону продлить. Перенести картинку в документ.

Как же писать квадратный, кубический и четвёртый корни?

Если вам нужно написать, к примеру, технический текст, возникает вопрос: «как написать символы, которых нет на клавиатуре?» Одним из таких символов является корень или радикал.

Наверняка вы замечали, что на многих сайтах используется этот обозначение. И это неудивительно, ведь подобными возможностями обладают все без исключения текстовые редакторы, а если быть точнее, суть вопроса заключается именно в клавиатуре.

Как написать корень на клавиатуре? – всё очень просто! Хоть знак «корень» на клавиатуре и не расположен, его всё-таки можно написать: для этого существует даже не один, а несколько способов. Рассмотрим их подробнее:

• Способ №1. Используя горячие клавиши клавиатуры (Alt-код, т.е. первая клавиша в коде — Alt).
• Способ №2. Используя 10-й код (HTML-код).
• Способ №3. Используя 16-й код (Юникод).

Обратите внимание! Для того чтобы воспользоваться способом №1, вы должны нажать и удерживать клавишу Alt, после чего начать ввод числового кода с использованием дополнительных цифровых клавиш (расположены на правой части клавиатуры). Перед тем как ввести числовой код, убедитесь, что цифровые клавиши включены (индикатор NumLk должен гореть)

10-й и 16-й коды можно не вводить, а просто скопировать из таблицы и вставить в том месте, где вам нужно

Перед тем как ввести числовой код, убедитесь, что цифровые клавиши включены (индикатор NumLk должен гореть). 10-й и 16-й коды можно не вводить, а просто скопировать из таблицы и вставить в том месте, где вам нужно.

Дискриминант: формула корней квадратного уравнения

Чтобы найти результат квадратного уравнения, придумали формулу корней. Выглядит она так:

где D = b2 − 4ac — дискриминант квадратного уравнения.

Эта запись означает:

Чтобы легко применять эту формулу, нужно понять, как она получилась. Давайте разбираться.

Выводим формулу корней квадратного уравнения

Продолжим изучать формулу корней квадратного уравнения.

Пусть перед нами есть задача решить квадратное уравнение ax2 + bx + c = 0. Выполним ряд равносильных преобразований:

• разделим обе части этого уравнения на отличное от нуля число a, после чего получим приведенное квадратное уравнение:
• выделим полный квадрат левой части нового уравнения:

  ,

  после чего уравнение примет вид

• перенесем два последних слагаемых в правую часть и сменим знак на противоположный:
• преобразуем выражение в правой части:

Так, мы пришли к уравнению , которое полностью равносильно исходному ax2 + bx + c = 0.

Отсюда выводы про корни уравнения :

И еще один вывод: есть у уравнения корень или нет, зависит от знака выражения в правой части

При этом важно помнить, что знак этого выражения задается знаком числителя. Потому выражение принято называть дискриминантом квадратного уравнения и обозначается буквой D

По значению и знаку дискриминанта можно сделать вывод, есть ли действительные корни у квадратного уравнения, и сколько.

Повторим:

Алгоритм решения квадратных уравнений по формулам корней

Теперь мы знаем, что при решении квадратных уравнения можно использовать универсальную формулу корней — это помогает находить комплексные корни.

В 8 классе на алгебре можно встретить задачу по поиску действительных корней квадратного уравнения

Для этого важно перед использованием формул найти дискриминант и убедиться, что он неотрицательный, и только после этого вычислять значения корней. Если дискриминант отрицательный, значит уравнение не имеет действительных корней

Алгоритм решения квадратного уравнения ax2 + bx + c = 0:

• вычислить его значение дискриминанта по формуле D = b2−4ac;
• если дискриминант отрицательный, зафиксировать, что действительных корней нет;
• если дискриминант равен нулю, вычислить единственный корень уравнения по формуле х = — b2/2a;
• если дискриминант положительный, найти два действительных корня квадратного уравнения по формуле корней

Чтобы запомнить алгоритм решения квадратных уравнений и с легкостью его использовать, давайте тренироваться!

Примеры решения квадратных уравнений

Как решать квадратные уравнения мы уже знаем, осталось закрепить знания на практике.

Пример 1. Решить уравнение −4×2 + 28x — 49 = 0.

Как решаем:

1. Найдем дискриминант: D = 282 — 4(-4)(-49) = 784 — 784 = 0
2. Так как дискриминант равен нулю, значит это квадратное уравнение имеет единственный корень
3. Найдем корень

   х = — 28/2(-4)

   х = 3,5

Ответ: единственный корень 3,5.

Пример 2. Решить уравнение 54 — 6×2 = 0.

Как решаем:

1. Произведем равносильные преобразования. Умножим обе части на −1

   54 — 6×2 = 0 | *(-1)

   6×2 — 54 = 0

2. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   6×2 = 54

   х2 = 9

   х = ±√9

   х₁ = 3, х₂ = — 3

Ответ: два корня 3 и — 3.

Пример 3. Решить уравнение x2— х = 0.

Как решаем:

1. Преобразуем уравнение так, чтобы появились множители

   х(х — 1) = 0

   х₁ = 0, х₂ = 1

Ответ: два корня 0 и 1.

Пример 4. Решить уравнение x2— 10 = 39.

Как решаем:

1. Оставим неизвестное в одной части, остальное перенесем с противоположным знаком в другую

   x2— 10 = 39

   x2= 39 + 10

   x2= 49

   х = ±√49

   х₁ = 7, х₂ = −7

Ответ: два корня 7 и −7.

Пример 5. Решить уравнение 3×2— 4x+94 = 0.

Как решаем:

1. Найдем дискриминант по формуле

   D = (-4)2 — 4 * 3 * 94 = 16 — 1128 = −1112

2. Дискриминант отрицательный, поэтому корней нет.

Ответ: корней нет.

В школьной программе за 8 класс нет обязательного требования искать комплексные корни, но такой подход может ускорить ход решения. Если дискриминант отрицательный — сразу пишем ответ, что действительных корней нет и не мучаемся.

Приходите решать примеры на бытовых ситуациях, с красочными героями и в интерактивном формате. Запишите вашего ребенка на бесплатный пробный урок в онлайн-школу Skysmart: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.

Как написать корень на клавиатуре используя таблицу символов

Альтернативой этому варианту является использование специальной таблицы символов, имеющейся в ОС Виндовс.

1. Нажмите на «Пуск», затем выберите «Все программы»;
2. Потом «Стандартные», затем «Служебные», где выберите «Таблица символов».
3. Там найдите знак корня √, кликните на него, нажмите на кнопку «Выбрать», затем «Копировать» и скопируйте его в нужный вам текст с помощью клавиш Ctrl+V.

Таблица символов В текстовом редакторе Word (а также в Excel) также имеется соответствующая таблица символов, которую можно использовать для наших задач. Вы можете найти её, перейдя во вкладку «Вставка», и нажав на «Символ» справа, а затем и кликнув на надпись «Другие символы» чуть снизу, это поможет вам в решении вопроса написании корня в Ворде.

Можно, также, использовать опцию «Формула» во вкладке «Вставка» по описанному в данном ролике алгоритму.

Что такое корень и его назначение

В общих чертах его знак похож на латинскую букву V, с тем лишь отличием, что правая часть длиннее левой. Связано это с тем, что справа пишется число большее, чем левое. И как было сказано выше – левое часто не пишут (если речь идет о квадратном корне).

1. Пример 1. √16 = 4. Полная запись выглядела бы так: 2√16 = 4. Как видно из примера, двойка по умолчанию не пишется. Она обозначает то, сколько раз число 4 было умножено на само себя. Иными словами – 4, умноженное на 4 равняется числу 16.
2. Пример 2. 3√8 = 2. Тут уже вычисляется кубический корень (третьей степени). Число 8 получается из умножения числа 2 на само себя три раза – 2*2*2 = 8.

Как же писать квадратный, кубический и четвёртый корни?

Если вам нужно написать, к примеру, технический текст, возникает вопрос: «как написать символы, которых нет на клавиатуре?» Одним из таких символов является корень или радикал.

Наверняка вы замечали, что на многих сайтах используется этот обозначение. И это неудивительно, ведь подобными возможностями обладают все без исключения текстовые редакторы, а если быть точнее, суть вопроса заключается именно в клавиатуре.

Как написать корень на клавиатуре? – всё очень просто! Хоть знак «корень» на клавиатуре и не расположен, его всё-таки можно написать: для этого существует даже не один, а несколько способов. Рассмотрим их подробнее:

• Способ №1. Используя горячие клавиши клавиатуры (Alt-код, т.е. первая клавиша в коде — Alt).
• Способ №2. Используя 10-й код (HTML-код).
• Способ №3. Используя 16-й код (Юникод).

Обратите внимание! Для того чтобы воспользоваться способом №1, вы должны нажать и удерживать клавишу Alt, после чего начать ввод числового кода с использованием дополнительных цифровых клавиш (расположены на правой части клавиатуры). Перед тем как ввести числовой код, убедитесь, что цифровые клавиши включены (индикатор NumLk должен гореть)

10-й и 16-й коды можно не вводить, а просто скопировать из таблицы и вставить в том месте, где вам нужно

Перед тем как ввести числовой код, убедитесь, что цифровые клавиши включены (индикатор NumLk должен гореть). 10-й и 16-й коды можно не вводить, а просто скопировать из таблицы и вставить в том месте, где вам нужно.

√ Квадратный корень Alt + 251 √ √∛ Кубический корень — ∛ ∛∜ Четвертый корень — ∜ ∜

Теперь вы знаете, как писать корень на клавиатуре – для этого нужно запомнить комбинацию “Alt+251”. Точнее, нужно удерживать клавишу Alt, после чего на цифровых клавишах нажать 2, 5, 1 и отпустить Alt.

Если вы всё сделали верно, на экране появится знак корня. Выглядит он следующим образом: √ (вы также можете просто скопировать его отсюда). Так самому можно писать и другие самые разные смайлики в ворде и других текстовых редакторах.

Вы можете воспользоваться и помощью поисковика Google. Для этого просто введите в поиск то, что вы ищите (к примеру, знак корня), после чего просто его скопировать.

Если у вас возникли какие-либо проблемы (на вашем ноутбуке нет расположенных справа цифровых клавиш и т. д.), достаточно нажать Пуск и перейти в таблицу символов. В зависимости от Windows таблица символов может находиться как в разделе с приложениями, так и в разделе «Стандартные».

Источник статьи: http://hitech.buyon.ru/pages/kak-pishetsya-koren-na-kompyutere/

Как написать корень на клавиатуре используя таблицу символов

Альтернативой этому варианту является использование специальной таблицы символов, имеющейся в ОС Виндовс.

1. Нажмите на «Пуск», затем выберите «Все программы»;
2. Потом «Стандартные», затем «Служебные», где выберите «Таблица символов».
3. Там найдите знак корня √, кликните на него, нажмите на кнопку «Выбрать», затем «Копировать» и скопируйте его в нужный вам текст с помощью клавиш Ctrl+V.

В текстовом редакторе Word (а также в Excel) также имеется соответствующая таблица символов, которую можно использовать для наших задач. Вы можете найти её, перейдя во вкладку «Вставка», и нажав на «Символ» справа, а затем и кликнув на надпись «Другие символы» чуть снизу, это поможет вам в решении вопроса написании корня в Ворде.

Можно, также, использовать опцию «Формула» во вкладке «Вставка» по описанному в данном ролике алгоритму.

Как найти квадратный корень из числа

Квадратные корни из целых чисел, чьи квадраты известны, вычислить довольно просто.
Для этого достаточно выучить таблицу квадратов.

Чаще всего в задачах школьного курса математики требуется найти квадратный корень из квадратов чисел от
до .

№ 307 Алимов 9 класс

Вычислить арифметический квадратный корень из числа.

Как найти квадратный корень из десятичной дроби

Важно!

При нахождении квадратного корня из десятичной дроби нужно выполнить следующие действия:

1. забыть про запятую в исходной десятичной дроби и представить её в виде целого числа;
2. вычислить для целого числа квадратный корень;
3. полученное целое число заменить на десятичную дробь (поставить запятую исходя из
   правила умножения десятичных дробей).

Более подробно разберем на примере ниже.

№ 307 Алимов 9 класс

Вычислить квадратный корень из десятичной дроби «».

По первому пункту правила забудем про запятую в десятичной дроби и представим ее в виде целого числа «».

Нетрудно вспомнить, какое число в квадрате дает «». Это число
«».

Вспомним правило умножения десятичных дробей.
Количество знаков после запятой в результате умножения десятичных дробей равняется сумме количества знаков после запятой каждой
дроби.

Т.е., например, при умножении «» на
«» в полученном произведении будет десятичная дробь с тремя знаками после запятой.

Значит, при вычислении квадратного корня

нам нужно найти десятичную дробь, у которой был бы только один знак после запятой.

Мы исходим из того, что в результате умножения десятичной дроби на саму себя в результате должно было получиться
два знака после запятой, как у десятичной дроби «».

Получается, что ответ — десятичная дробь «».

Убедимся, что квадрат десятичной дроби
«» дает
«».

Умножим в столбик «» на

«».

Рассмотрим другой пример вычисления квадратного корня из десятичной дроби. Вычислить:

Представим вместо десятичной дроби «» целое число
«». Какое число в квадрате даст «»?
Ответ — число «».

Т.к. в десятичной дроби «» — два знака после запятой, значит в десятичной дроби,
которая дала в квадрате «» должен быть один знак после запятой.

Убедимся, что «» дает в квадрате «».

Квадратные корни из чисел

и т.п.

Не из всех чисел удается легко извлечь квадратный корень. Например, совершенно неочевидно, чему равен

или

и т.п.

В самом деле, какое число в квадрате даст «»? Или число «»?
Такое число не будет целым. Более того, оно представляет из себя
непериодическую десятичную дробь
и входит в
множество иррациональных чисел.

Что делать, когда в ответе остаются подобные квадратные корни? Как, например, в примере ниже:

Нет такого целого числа, которое бы дало в квадрате число «».
Поэтому, перед завершением задачи внимательно читайте её условие.

Если в задаче дополнительно ничего не сказано об обязательном вычислении всех квадратных корней, тогда ответ можно
оставить с корнем.

Если в задании сказано, что необходимо вычислить все квадратные корни с помощью микрокалькулятора,
то после вычисления квадратного корня на калькуляторе
округлите результат до необходимого количества знаков.

Текст задания в таком случае может быть написан следующим образом:

«Вычислить. Квадратные корни найти с помощью калькулятора и округлить с точностью до
«».

Как написать квадратный корень

Рассмотрим несколько способов написания знака квадратного корня на клавиатуре — в любом приложении или только в Word.

На клавиатуре, используя NUM-блок

Самый простой способ написать квадратный корень — это использовать NUM-блок на клавиатуре, который позволяет путем ввода определенных комбинаций получать различные знаки.

Напомним: NUM-блок — это блок в правой части полномасштабной клавиатуры (на ноутбучных клавиатурах он бывает расположен в другом месте или активироваться на других клавишах при нажатии NUM LOCK).

Убедитесь, что NUM-блок активирован, для этого нажмите клавишу NUM LOCK. Обычно на клавиатуре есть светодиоды, которые горят, когда NUM-блок активирован.

После этого переключите раскладку клавиатуры на английскую, зажмите клавишу Alt и введите комбинацию 251 (на NUM-блоке).

Когда вы отпустите кнопку Alt, появится знак корня: √

Таким образом квадратный корень можно ввести практически в любой программе.

Используя таблицу символов

В операционной системе Windows для случаев, когда необходимо написать особый символ, есть специальная таблица с этими символами. Чтобы ее вызвать, введите в поиске слова “Таблица символов” и запустите найденное приложение.

Найдите в списке доступных символов знак квадратного корня — он находится во второй половине таблицы.

Обратите внимание
Единожды отыскав знак корня, потом повторно его искать будет легче.

Когда найдете нужный символ, нажмите на него, далее нажмите “Выбрать” и “Копировать”.

После этого у вас в буфере обмена будет квадратный корень. Теперь его можно вставить в любую программу обычным способом — нажать правой кнопкой на место для ввода символов и выбрав “Вставить”.

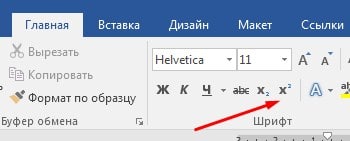
В Word через список символов

Похожая таблица символов есть и в Word, и ею тоже можно воспользоваться чтобы вставить значок квадратного корня в текст. Для этого переключитесь в программе в верхнем меню на пункт “Вставка”, выберите вариант “Символ” и нажмите “Другие символы”.

Откроется почти такая же таблица, как была рассмотрена выше, за одним лишь исключением — здесь более удобный поиск. Выберите сверху набор “Математические операторы”, и вы быстро найдете в списке символов квадратный корень. Нажмите на него и выберите пункт “Вставить”.

После этого в тексте появится знак корня.

Обратите внимание
Этот знак корня можно использовать для копирования в другие программы. Просто выделите его, нажмите правой кнопкой и выберите “Копировать”, а потом вставьте в нужном приложении.

В Word вставить формулу от числа

Еще один способ добавить знак квадратного корня в Word — это использовать вставку формулы. Подойдет такой вариант, если не нужно, чтобы корень квадратный был встроен внутрь текста.

Вставка квадратного корня через формулу выполняется следующим образом. Нажмите в Word раздел “Вставка” и выберите “Формула”.

Далее нажмите “Радикал”.

Выберите вариант вставки квадратного корня от числа.

Остается только ввести число от которого будет отображаться квадратный корень.

Обратите внимание
Через вставку формулы можно вставить и обычный квадратный корень, не указывая от какого числа он берется. Для этого нужно после выбора пункта “Формула” в разделе “Вставка” сверху выбрать в списке доступных вариантов значок обычного квадратного корня.

Применение

Разумный вопрос, который рано или поздно возникает у человека, только начавшего изучать математику – зачем вообще нужен квадратный корень? Конечно, он, может, никогда и не пригодится уборщице тёте Люсе или дворнику дяде Васе, но для более образованного человека квадратный корень всё же нужен.

Начнём с того, что квадратный корень нужен для вычисления диагонали прямоугольника. Ну и что с того? – спросят многие. А с того, что это нужно для качественного ремонта, чтобы правильно и аккуратно разложить линолеум, сделать навесной потолок и для проведения многих других работ в сфере строительства.

Корни из произведения и частного

Перед тем как давать какие-либо новый формулы, напомню важный факт. Корень из суммы не равен сумме корней:

Иначе мы бы получили вот такие бредовые выкладки:

Вроде бы, капитаноочевидно, но многие даже в старших классах допускают такие ошибки.

А теперь разберём ещё два свойства корней.

2.1. Умножение и деление корней

Корни можно умножать и делить. Правила просты:

Примеры:

Попробуйте сами:

Задание 3. Найдите значение выражения:

Как видите, с помощью формул мы разбиваем сложный корень на несколько простых.

Мы знаем, то все формулы работают как слева-направо, так и справа-налево, поэтому корни можно «склеивать». При этом новый корень может легко вычисляться, хотя исходные части — не вычисляются вообще. Например:

Попробуйте повторить этот трюк:

Задание 4. Найдите значение выражения:

2.2. Проблемы с областью определения

Но есть одна тонкость. Взгляните, например, на формулу произведения корней:

Напомню: знак радикала обозначает арифметический квадратный корень, который извлекается только из неотрицательных чисел и сам является числом неотрицательным.

С левой стороны от знака равенства стоит один корень, а справа — целых два. Поэтому области определения левой и правой части этого равенства различны:

В чём конкретно состоит различие?

В первой строке мы видим произведение, поэтому неравенство (1) верно всякий раз, когда знаки множителей совпадают. В частности, оба множителя могут быть отрицательными, но их произведение всё равно будет положительным.

Вторая строка — система из двух неравенств, и здесь отрицательные числа нас уже не устроят. Вывод:

Красным я выделил ситуацию, которая допустима для корня из произведения, но становится недопустимой для произведения корней.

Поскольку любое равенство определено лишь тогда, когда определена и левая, и правая его части, дополним исходные правила специальными требованиями:

И вот в таком виде их уже можно использовать — везде и всегда!

Может показаться, что эти ограничения несущественны. Или искусственны. Чуть выше мы никак их не учитывали и всё прекрасно посчитали. Поэтому вопрос: когда ограничения области определения становятся существенным?

Ответ: когда под корнями стоят не конкретные числа, а переменные. К примеру, пусть даны числа:

Очевидно, что произведение двух отрицательных чисел будет положительным. И хотя корень из произведения будет определён, извлекать корни из отдельных множителей нельзя:

Значит, нужно сделать так, чтобы множители под корнем стали положительными. И тут нам на помощь приходит старое доброе число −1:

Добавление минусов к каждому из двух множителей нисколько не повлияло на произведение, но привело к возникновению двух новых множителей, каждый из которых уже точно положителен:

Помните об этом преобразовании, когда сталкиваетесь с произведением отрицательных выражений под знаком корня. Источником такой отрицательности могут быть условия задачи, либо следствия из области определения (такое часто встречается в логарифмических уравнениях и неравенствах, которые изучаются в 10—11 классах).

Ну а мы немного потренируемся и пойдём к третьей части урока — работе с переменными.

Задание 5. Найдите значение выражения:

Переходим к самому весёлому.:)

Как набирать

Знак корня на клавиатуре

В электронном виде этот символ может понадобиться как студентам, учителям, научным деятелям. Связано это может быть с докладом, проектом, рефератом и так далее. В стандартной раскладке клавиатуры нет символа квадратного корня, так как он не является популярным или часто используемым. Но его можно набрать и другими способами.

Самые распространённые программы для работы с документами – это пакет MS Office, в частности, Microsoft Word. Набрать квадратный корень в этой программе можно несколькими способами, которые по аналогии могут подойти и к другим программам, с небольшими различиями в интерфейсе.

Способы набора символа в Ворде

Можно использовать следующие варианты:

• При помощи набора специального кода . В самом низу клавиатуры находится клавиша с названием Alt. Этих клавиш две, подойдёт любая из них. В правой части клавиатуры есть цифры, над которыми находится клавиша Num Lock. Эту клавишу нужно предварительно нажать, чтобы активировать цифры, находящиеся под ней. Затем зажимаем клавишу Alt и не отпуская клавишу, набираем: 251. После этого на экране появится нужный значок.
• Ещё один способ связан с меню «вставка-символ». После того как будет найден нужный знак, его можно будет повторять, как ранее использованный. Его код в меню поиска — 221A, (латинская буква). Предварительно лучше включить Юникод.
• Самый «красивый» символ набирается с помощью компонента Microsoft Equation 3.0. Для этого надо зайти в «вставка-объект-Microsoft Equation 3.0», после чего найти там нужный знак и использовать его. При этом методе знак смотрится лучше всего, так как тут он отображается правильно с типографической и математической точки зрения.

Не получили ответ на свой вопрос? Предложите авторам тему.

Школьники или студенты в наше время часто работают в текстовом редакторе «Ворд». Однако ввиду недостаточной осведомленности некоторые задачи в нем они не способны выполнить. Особенно сложно работать с математическими символами, ведь на клавиатуре их недостаточно. В этой статье пойдет речь о знаке корня. Будет рассказано, как вставить его в документ. Продемонстрировано будет четыре разных способа, а по итогу прочтения статьи пользователь решит для себя сам, каким из них пользоваться.

Способ 3: «Командная строка»

Квадратные корни из натуральных чисел

Положительное число имеет два квадратных корня, один положительный, и отрицательный, которые противоположны друг другу. Когда речь идет о на квадратный корень из положительного целого числа, то, как правило , положительный квадратный корень , который имел в виду.

Квадратные корни из целого числа — это целые алгебраические числа, а точнее — квадратичные целые числа .

Квадратный корень из положительного целого числа — это произведение корней его простых множителей, потому что квадратный корень из произведения — это произведение квадратных корней из множителей. Поскольку необходимы только корни тех простых чисел, которые имеют нечетную степень при факторизации . Точнее, квадратный корень из разложения на простые множители равен
п2kзнак равнопk,{\ displaystyle {\ sqrt {p ^ {2k}}} = p ^ {k},}

п12е1+1⋯пk2еk+1пk+12еk+1…пп2епзнак равноп1е1…ппепп1…пk.{\ Displaystyle {\ sqrt {p_ {1} ^ {2e_ {1} +1} \ cdots p_ {k} ^ {2e_ {k} +1} p_ {k + 1} ^ {2e_ {k + 1}} \ dots p_ {n} ^ {2e_ {n}}}} = p_ {1} ^ {e_ {1}} \ dots p_ {n} ^ {e_ {n}} {\ sqrt {p_ {1} \ dots p_ {k}}}.}

В виде десятичных разложений

Квадратные корни из полных квадратов (например, 0, 1, 4, 9, 16) являются целыми числами . Во всех остальных случаях квадратные корни из положительных целых чисел являются иррациональными числами и, следовательно, имеют неповторяющиеся десятичные дроби в их десятичных представлениях . Десятичные приближения квадратных корней из первых нескольких натуральных чисел приведены в следующей таблице.

п	п,{\ displaystyle {\ sqrt {n}},} усечено до 50 знаков после запятой
1	1
2	1,4142135623 7309504880 1688724209 6980785696 7187537694
3	1.7320508075 6887729352 7446341505 8723669428 0525381038
4	2
5	2,2360679774 9978969640 9173668731 2762354406 1835961152
6	2.4494897427 8317809819 7284074705 8913919659 4748065667
7	2,6457513110 6459059050 1615753639 2604257102 5918308245
8	2,8284271247 4619009760 3377448419 3961571393 4375075389
9	3
10	3,1622776601 6837933199 8893544432 7185337195 5513932521

Как расширения в других системах счисления

Как и раньше, квадратные корни из полных квадратов (например, 1, 4, 9, 16) являются целыми числами. Во всех остальных случаях квадратные корни из положительных целых чисел являются иррациональными числами и, следовательно, имеют неповторяющиеся цифры в любой стандартной позиционной системе обозначений .

Квадратные корни из малых целых чисел используются в схемах хэш-функций SHA-1 и SHA-2, чтобы ничего не дать мне в числах в рукаве .

Как периодические непрерывные дроби

Один из самых интригующих результатов изучения иррациональных чисел как цепных дробей был получен Джозефом Луи Лагранжем c. 1780. Лагранж обнаружил, что представление квадратного корня из любого положительного целого числа, не являющегося квадратом, в виде непрерывной дроби является периодическим . То есть определенный образец частичных знаменателей бесконечно повторяется в непрерывной дроби. В каком-то смысле эти квадратные корни являются простейшими иррациональными числами, потому что они могут быть представлены простым повторяющимся шаблоном целых чисел.

2{\ displaystyle {\ sqrt {2}}}	=
3{\ displaystyle {\ sqrt {3}}}	=
4{\ displaystyle {\ sqrt {4}}}	=
5{\ displaystyle {\ sqrt {5}}}	=
6{\ displaystyle {\ sqrt {6}}}	=
7{\ displaystyle {\ sqrt {7}}}	=
8{\ displaystyle {\ sqrt {8}}}	=
9{\ displaystyle {\ sqrt {9}}}	=
10{\ displaystyle {\ sqrt {10}}}	=
11{\ displaystyle {\ sqrt {11}}}	=
12{\ displaystyle {\ sqrt {12}}}	=
13{\ displaystyle {\ sqrt {13}}}	=
14{\ displaystyle {\ sqrt {14}}}	=
15{\ displaystyle {\ sqrt {15}}}	=
16{\ displaystyle {\ sqrt {16}}}	=
17{\ displaystyle {\ sqrt {17}}}	=
18{\ displaystyle {\ sqrt {18}}}	=
19{\ displaystyle {\ sqrt {19}}}	=
20{\ displaystyle {\ sqrt {20}}}	=

Квадратная скобка обозначение , используемое выше , является краткой формой для непрерывной дроби. Написанная в более сложной алгебраической форме, простая непрерывная дробь для квадратного корня из 11, , выглядит так:

11знак равно3+13+16+13+16+13+⋱{\ displaystyle {\ sqrt {11}} = 3 + {\ cfrac {1} {3 + {\ cfrac {1} {6 + {\ cfrac {1} {3 + {\ cfrac {1} {6+ {) \ cfrac {1} {3+ \ ddots}}}}}}}}}}}

где двузначный образец {3, 6} повторяется снова и снова в частичных знаменателях. Так как 11 = 3 2 + 2 , выше, также идентичен следующие :

11знак равно3+26+26+26+26+26+⋱знак равно3+620-1-120-120-120-120-⋱.{\ displaystyle {\ sqrt {11}} = 3 + {\ cfrac {2} {6 + {\ cfrac {2} {6 + {\ cfrac {2} {6 + {\ cfrac {2} {6+ { \ cfrac {2} {6+ \ ddots}}}}}}}}} = 3 + {\ cfrac {6} {20-1 — {\ cfrac {1} {20 — {\ cfrac {1} { 20 — {\ cfrac {1} {20 — {\ cfrac {1} {20- \ ddots}}}}}}}}}}.}