Как находить проценты от числа

Как вычислить на сколько процентов увеличилась или уменьшилась сумма

Это можно сделать способом, указанным в первом пункте способом: вычислить, сколько составляет 1%, затем получить разницу между данными (вычитать большую цифру из меньшей) и поделить ее на результат.

Пример: нужно вычислить, на сколько уменьшилось 200, если оно стало 150.

1. 200 – это 100%, 1% = 200/100 = 2.
2. 200-150 = 50.
3. 50/2 = 25, то есть 150 увеличилось на 25%.

Если необходимо посчитать, на сколько увеличилось, потребуется слегка изменить вычисления:

1. 150 – это 100%, то есть 1% =150/100 = 1,5.
2. 200-150 = 50.
3. 50/1,5 = 33,3%.

Стоит учесть: поскольку в первом случае цифра уменьшалась, а во втором – увеличилась, результаты тоже получились разными.

Чтобы вычислить отношение между увеличивающимися цифрами, можно воспользоваться еще одним способом. Для этого итоговое значение нужно разделить на начальное и посмотреть на три цифры после запятой. Переписав их отдельно и поставив запятую после первых двух, получим результат.

Лучше всего принцип действия виден на примере: нужно отыскать, на сколько увеличилась цифра, если из 150 она превратилась в 200.

1. 200/150 = 1,33333…
2. Три знака после запятой – это «333». Отделив первые две цифры, получим «33,3%».

Пример 2: из 100 получилось 110.

1. 110/100 = 1,1 или 1,100.
2. 100 – это 10,0%.

Вычисление процентов может потребоваться при разных подсчетах: для определения суммы налога, кредита, чтобы рассчитаться с клиентами по счету и т.д. Провести вычисления можно разными способами, выбрав наиболее понятный и простой.

Смотрите видео, в котором объясняется, как оперативно высчитать процент от суммы без калькулятора:

Как использовать калькулятор процентов

Кроме обычного соотношения чисел и их процентного эквивалента, с помощью калькулятора можно провести простые математические вычисления увеличения или уменьшения заданного числа на количество процентов. Для этого достаточно заполнить соответствующие поля и нажать на кнопку “Рассчитать”.

Например, чтобы узнать сколько составит 5% от числа 80, ставим значения внужные поля. После нажатия кнопки расчета получим результат “4”.

Точно также калькулятор посчитает в каком процентном соотношении находятся два разных числа. Например 80 к 100 составит 80%.

С помощью калькулятора можно

• прибавить % — если к числу 80 прибавить 5%, то получим 84;
• вычесть % — если от числа 80 вычесть 5%, то получим 76.

Такие вычисления нужны, как для работы, так и в обычной жизни.

1. В магазине, когда мы видим на ценнике скидку 35%, калькулятор поможет быстро посчитать, какую сумму фактически надо заплатить.
2. На кухне, когда готовим блюдо, часто надо делать пересчет при изменении количества порций.
3. На работе, например в магазине, когда надо проанализировать соотношение выручки от нескольких продавцов, чтобы оценить качество работы. Также понадобится подсчет процентов для определения нагрузки, допустим почасовой, еженедельной и т.д.
4. Когда есть необходимость получения кредита. Вычисление суммы, которую включает процентная ставка, поможет подобрать наиболее выгодный вариант. То же касается и депозитов.
5. Не обойтись без процентов и копирайтерам. Любой заказчик хочет получить 100% уникальность при низком спаме и водности текста.

Насколько число меньше другого в процентах

К примеру: обычная стоимость порошка – 500 рублей. По акции, цену снизили до 480 рублей. Насколько цена по акции, меньше первоначальной в процентах? Вначале находят процентную составляющую акционной цены от базовой, а затем находиться их разница. Составляем пропорцию:

Вычисляем по формуле: (480*100)/500=96. 100%-96%=4%. Цена по акции меньше первоначальной на 4%.

Насколько число больше другого в процентах. Пример: клавиатура стоила 300 рублей, а после повышения курса доллара, цена выросла до 390 рублей. Насколько изменилась цена на клавиатуру в процентах? Вначале находиться общая процентная ставка новой цены, относительно первоначальной, затем вычисляется их разница. Составляем пропорцию:

Вычисляем по формуле: (390*100)/300=130. 130%-100%=30%. Цена выросла на 30%.

Неизвестное число больше известного на определенный процент. Пример: товар в магазине, дороже товара на складе на 15%.  Цена сахара на складе – 50 рублей и приравнивается к 100%. Магазинная цена  – 100%+15%=115%. Вычисляем по формуле: (115*50)/100=57,5

Неизвестное число меньше известного на заданный процент. Пример: оптом на 5% дешевле. Цена за розницу – 60 рублей и равна 100 процентам, за опт – 100%-5%=95%. Составляем пропорцию:

Вычисляем по формуле: (60*95)/100=57

Процент между двумя числами. Ситуация, когда известно число, составляющее 100% и число, составляющее некую долю от первоначального. Пример: ожидалась партия в 60 коробок, а завезли 53. На сколько процентов выполнился план. Составляем пропорцию:

Вычисляем по формуле: (53*100)/60=88,3

Самая сложная «задача» — не запутаться в составлении пропорции.

Расчет при помощи пропорций

Этот способ высчитывания известен всем со школьной программы.

Расчет применяют в случаях, когда необходимо высчитывать процентное соотношение между двумя данными. Иначе говоря, если одно число представляет собой 100%, то сколько будет составлять второе?

Например, Х (икс) – это 100%, Y – это n%. Для вычисления значения n необходимо записать пример в следующем виде:

X = 100.

Y = n.

Перемножив числа по диагоналям, получим пропорцию:

X*n = Y*100.

n = (Y*100)/X.

Пример.

Нужно посчитать, какую долю от 500 составят 25.

1. 500 = 100%, 25 = n%.
2. n = (25*100)/500 = 5%.

Обратите внимание: в этих случаях Y должно быть меньше Х, иначе результат получится больше 100%.

Если нужно получить число, которое составляет какую-либо часть, потребуется воспользоваться обратной формулой:

Y = (n*X)/100.

Пример.

Нужно подсчитать, сколько будет 5% от 500.

Y = (5*500)/100 = 25.

Считаем процент от суммы вклада

Напомню, что проценты по банковскому вкладу могут быть простыми и сложными.

В первом случае банк начисляет доход на начальную сумму депозита. То есть, каждый месяц/квартал/год вкладчик получает от банка один и тот же «бонус».

Схема со сложными процентами для вкладчика выгоднее. Начисленный за месяц доход «плюсуется» к сумме вклада. И уже в следующем периоде процент будет насчитываться на большую сумму. А в следующем – на еще большую и так далее. На «длинных» сроках (10-20 лет) сложные проценты творят настоящие чудеса!

Конечно, формулы расчета для простых и сложных процентов отличаются друг от друга.

Рассмотрим их на конкретном примере.

Доходность по вкладу с простыми процентами

Сумма % = (вклад*ставка*дней в расчетном периоде)/(дней в году*100)

Пример. Валера открыл вклад на сумму 20 000 рублей под 9% годовых на один год.

Рассчитаем доходность вклада за год, месяц, неделю и один день.

Сумма процентов за год = (20 000*9*365)/(365*100) = 1800 рублей

Понятно, что в нашем примере годовую доходность можно было посчитать гораздо проще: 20 000*0,09. И в результате получить те же самые 1800 рублей. Но раз решили считать по формуле, то и будем считать по ней. Главное – понять логику.

Сумма процентов за месяц (июнь) = (20 000*9*30)/(365*100) = 148 рублей

Сумма процентов за неделю = (20 000*9*7)/(365*100) = 34,5 рублей

Сумма процентов за день = (20 000*9*1)/(365*100) = 5 рублей

Согласитесь, формула простых процентов элементарна. Она позволяет рассчитать доходность по вкладу за любое количество дней.

Доходность по вкладу со сложными процентами

Усложняем пример. Формула расчета сложных процентов уж чуть «мудреней», чем в предыдущем варианте. Калькулятор должен иметь функцию «степень». Как вариант, можно использовать опцию степень в таблице Excel.

• Сумма % = вклад*(1+ ставка за период капитализации)число капитализаций — вклад
• Ставка за период капитализации = (годовая ставка*дни в периоде капитализации)/(число дней в году*100)

Вернемся к нашему примеру. Валера разместил на банковском вкладе те же 20 000 рублей под 9% годовых. Но в этот раз — с ежемесячной капитализацией процентов.

Сначала посчитаем ставку за период капитализации. По условиям вклада проценты начисляются и «плюсуются» к депозиту один раз в месяц. Значит, в периоде капитализации у нас 30 дней.

Таким образом, ставка за период капитализации = (9*30)/(365*100) = 0,0074%

А теперь считаем, сколько наш вклад принесет в виде процентов за разные периоды.

Сумма процентов за год = 20 000*(1+0,0074) 12 – 20 000 = 1 850 рублей

В степень «12» мы возводим, потому что год включает двенадцать периодов капитализации.

Как видите, даже на такой символической сумме и коротком сроке разница в доходности вклада с простыми и сложными процентами составляет 50 рублей.

Сумма процентов за полгода = 20 000*(1+0,0074) 6 – 20 000 = 905 рублей

Сумма процентов за квартал = 20 000*(1+0,0074) 3 – 20 000 = 447 рублей

Сумма процентов за месяц = 20 000*(1+0,0074) 1 – 20 000 = 148 рублей

Вкладчик получит все те же 148 рублей и с простыми, и со сложными процентами. Расхождения в доходности начнутся со второго месяца. И чем длиннее срок депозита – тем существенней будет разница.

Пока мы не отошли далеко от темы сложных процентов, давайте проверим, насколько справедлива одна из рекомендаций финансовых консультантов. Я имею в виду совет выбирать вклады с капитализацией процентов не раз в полгода или квартал, а раз в месяц.

Предположим, наш условный Валера оформил депозит на ту же сумму, срок и под ту же ставку, но с капитализацией процентов раз в полгода.

Для начала нам придется пересчитать ставку за период капитализации. Ведь теперь этот период составляет не 30 дней (месяц), а 182 дня (полгода).

Ставка = (9*182)/(365*100) = 0,0449%

Теперь считаем доходность по вкладу за год.

Сумма процентов за год = 20 000*(1+0,0449) 2 – 20 000 = 1 836 рублей

Вывод: при прочих равных условиях полугодовая капитализация принесет Валере на 14 рублей меньше, чем ежемесячная (1850 – 1836).

Понимаю, что разница совсем невелика. Но ведь и другие исходные данные у нас символические. На крупных суммах и длинных сроках 14 рублей превратятся в тысячи и миллионы.

Обратное вычисление

Очень часто в вопросе о том, как посчитать процент от суммы, возникает и недвусмысленный обратный перевод. На практике это связано, скажем, с обратным вычислением четверти. Всем известно, что этот показатель составляет 25% от начального числа. Пусть, например, цену товара увеличили на 25%, что составило 25 рублей. Нужно найти, сколько стал стоить данный товар. Вот теперь попробуем разобраться, как вычислить не первоначальное число, зная значение процента, а всю сумму, которая должна получиться в конечном итоге. Казалось бы, решение простое:

25 = 25% (1/4 или 0,25);

Нет, абсолютно неверно. Так можно получить только изначальное число, без учета 25%. Для расчета всей суммы с учетом 25% нужно использовать формулу:

Или 100/0,8, что и покажет значение 125 (100 + 25), поскольку 100% плюс 25% в выражении единицы является числом 1,25 (единица плюс четвертая часть), а в обратном виде (1/x) – это именно 0,8. Произведя вычисления, получим, что х = 125.

Увеличение, уменьшение числа на заданное количество процентов

Школьники должны усвоить, что такое проценты, как считать их и решать разнообразные задачи. Для этого нужно понимать, как увеличивается или уменьшается число на N%.

Зачастую даются задания, да и в жизни нужно узнать, чему будет равно число, увеличенное на заданное количество процентов. К примеру, дано число Х. Нужно узнать, чему будет равно значение Х, если его увеличить, допустим, на 40%. Сначала нужно перевести 40% в дробное число (40/100). Итак, результатом увеличения числа Х станет: Х + 40% ∙ Х= (1+40/₁₀₀) ∙ Х = 1,4 ∙ Х. Если вместо Х подставить любое число, возьмем, к примеру, 100, тогда все выражение будет равно: 1,4 ∙ Х = 1,4 ∙ 100 = 140.

Примерно тот же принцип используется и при уменьшении числа на заданное число процентов. Нужно провести расчеты: Х — Х ∙ 40% = Х ∙ (1-40/₁₀₀) = 0,6 ∙ Х. Если величина равна 100, тогда 0,6 ∙ Х = 0,6 . 100 = 60.

Встречаются задания, где нужно узнать, на сколько процентов увеличилось число.

К примеру, дана задача: Машинист ехал по одному участку пути со скоростью 80 км/ч. На другом участке скорость поезда возросла до 100 км/ч. На сколько процентов возросла скорость поезда?

Решение:

Предположим, 80 км/ч – 100%. Тогда производим расчеты: (100% ∙ 100 км/ч) / 80 км/ч= 1000 : 8 = 125%. Получается, что 100 км/ч – это 125%. Чтобы узнать, на сколько увеличилась скорость, нужно вычислить: 125% — 100% = 25%.

Ответ: на 25% увеличилась скорость поезда на втором участке.

Как посчитать, сколько это процентов?

Этот вопрос задает каждый покупатель магазина, который намеревается воспользоваться акцией, и каждый сотрудник компании, желающий узнать размер своего вознаграждения за выполнение плана. Ведь проценты присутствуют во многих сферах повседневной жизни.

Возьмем конкретный пример. В магазине наушники стоили 3000 рублей, на них появилась акция в виде скидки 30%. Какая сумма вашей выгоды и сколько надо заплатить за товар?

Расчет простой

• 3000×30/100 = 900, поскольку 30/100 можно еще записать как 0,30, то
• 3000×0,30 = 900 рублей — это сумма скидки (30%) в денежном эквиваленте.

Теперь посчитаем сколько надо заплатить за наушники: 3000-900=2100 руб.

Расчет процентов — это не только задание на уроке в школе, но и актуальный вопрос для многих взрослых. Не у всех есть способность быстро выполнять действия в уме. Хотя рассчитать 10% или 20% от заданной суммы довольно просто, вычисление размера, например процентной ставки по банковским операциям иногда бывает проблематичным.

Что делать в этой ситуации? Вы можете прибегнуть к помощи специалиста, но проще применить свои навыки в использовании современных технологий и использовать онлайн калькулятор расчета процентов.

О легких и простых методах расчета процентов вы узнаете из видео.

Читайте далее:

Калькулятор автокредита: рассчитать процент переплаты

Онлайн конвертер долей, перевод дюжин, процентов, промилле и других единиц

Особенности ипотечного кредита: что нужно знать перед оформлением

Калькулятор сравнения шин, преимущества и недостатки изменения размера

Калькулятор расхода топлива, как рассчитать стоимость поездки

Как рассчитать доходность сделок по акциям, калькулятор расчета

Онлайн калькулятор

Если вы уже знакомы со всеми правилами и умеете их с легкостью использовать, но ситуация срочная и нужно все быстро посчитать — можно обратиться за помощью к калькулятору. Нахождение ответа выглядит так:

• Для подсчета % от суммы: вводим известное, равное 100%, знак умножения, нужный процент, знак %.
• Чтобы вычесть %: введем известное, равное 100%, знак минус, размер процентной доли и знак %.

5 класс, урок в самом разгаре, нужно определить процент от числа как можно быстрее — поможет онлайн калькулятор. Составлять расчет быстро и точно:

• Раз
• Два
• Три
• Четыре

Но помните, что на контрольных работах и экзаменах за вас никто не решит, а калькулятор не поможет.

Приходите практиковаться! В детской школе Skysmart ученики разбирают интересные задания, проходят квесты, играют в английский на интерактивной платформе и обсуждают темы, которые им интересны. Никаких скучных упражнений — только то, что зажигает вашего ребенка. Запишите его на бесплатный вводный урок и покажите, что английский может быть увлекательным путешествием!

Основные определения

Процент — это одна сотая часть от любого числа. Обозначающим знаком является %.

Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить известное на 100, как в примере выше.

А если нужно перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Например, 0,18 = 0,18 · 100% = 18%. Как перевести проценты в десятичную дробь — обратным действием: 18 : 100 = 0,18.

Выразить дробь в процентах просто. Для перевода сначала превратим её в десятичную дробь, а далее используем предыдущее правило.

Развивайте математическое мышление детей на наших уроках математики вместе с енотом Максом и его друзьями. Мы подобрали для вашего ребенка тысячи увлекательных заданий — от простых логических загадок до хитрых головоломок, над которыми интересно подумать. Все это поможет легче и быстрее подружиться со школьной математикой.

Примеры школьных заданий

Из запланированной дистанции в 32 км Том пробежал только 76%. Сколько километров пробежал мальчик?
Решение: для вычислений подходит первый калькулятор. В первую ячейку вставляем 76, во вторую — 32.
Получаем: Том пробежал 24.32 км.

Фермер Купер собрал с поля 500 кг кукурузы. 160 кг из этой массы оказалось неспелой. Сколько процентов от общего числа составила неспелая кукуруза?
Решение: для расчёта подходит второй калькулятор. В первое окошко записываем число 160, во второе — 500.
Получаем: 32% кукурузы оказалось неспелой.

Майкл прочитал своей подруге на ночь 112 страниц, что составляет 32% всей книги. Сколько страниц в книге?
Решение: используем для расчёта третий калькулятор. Вставляем в первую ячейку значение 112, а во вторую — 32.
Получаем: в книге 350 страниц.

Длина маршрута, по которому ходил автобус №42, составляла 48 километров. После добавления трёх дополнительных остановок расстояние от начальной до конечной станции изменилось до 78 километров. На сколько процентов изменилась длина маршрута?
Решение: используем для вычисления четвёртый калькулятор. В первую ячейку вбиваем число 78, во вторую — 48.
Получаем: длина маршрута выросла на 62.5%.

Братство металла и макулатуры в мае сдало на лом 320 кг цветного металла, а в июне на 30% больше. Сколько металла сдали ребята из братства в июне?
Решение: для расчёта будем использовать пятый калькулятор. В первую ячейку вставляем число 30, а во второе число 320.
Получаем: в июне братство сдало 416 кг металла.

Энди прорыл во вторник 3 метра туннеля, а в среду в связи с отъездом друга в Ирландию — на 22% меньше. Сколько метров туннеля прорыл Энди в среду?
Решение: в данном случае подходит шестой калькулятор. В первую ячейку вставляем 22, во вторую — 3.
Получаем: в среду мальчик прорыл 2.34 метра туннеля.

Задания для самостоятельного решения

Задание 1. Найдите 20% от числа 200

200 : 100 = 2 2 × 20 = 40

Задание 2. Найдите 34% от числа 1050

1050 : 100 = 10,5 10,5 × 34 = 357

Задание 3. Найдите 25% от числа 80

80 : 100 = 0,80 0,8 × 25 = 20

Задание 4. Найдите 185% от числа 1,5

1,5 : 100 = 0,015 0,015 × 185 = 2,775

Задание 5. Найдите 150% от числа 1150

1150 : 100 = 11,50 11,50 × 150 = 1725

Задание 6. Представьте выражение 15% в виде обыкновенной дроби

Задание 7. Представьте выражение 25% в виде обыкновенной дроби

Задание 8. Представьте выражение 125% в виде обыкновенной дроби

Задание 9. Число 12 это 60% от какого-то числа. Найдите это число.

12 : 60 = 0,2 0,2 × 100 = 20

Задание 10. Число 40 это 20% от какого-то числа. Найдите это число.

40 : 20 = 2 2 × 100 = 200

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Нахождения числа по его проценту

Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.

Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:

Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2

60 000 : 2 = 30 000

Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100

30 000 × 100 = 3 000 000

Мы нашли общую прибыль. Она составляет три миллиона.

Попробуем сформировать правило нахождения числа по его проценту.

Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.

Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.

Читаем первую часть правила:

Чтобы найти число по его проценту, нужно известное число разделить на данный процент

У нас известное число это 35, а данный процент это 7. Разделим 35 на 7

35 : 7 = 5

Читаем вторую часть правила:

и полученный результат умножить на 100

У нас полученный результат это число 5. Умножим 5 на 100

5 × 100 = 500

500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35

500 : 100 = 5

5 × 7 = 35

Получили 35. Значит задача была решена правильно.

Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.

Например, предыдущая задача может быть изложена так: число 35 это от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100

35 : 7 = 5

5 × 100 = 500

В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.

Быстрое вычисление процентов

Конечно, вычисление процентов при помощи пропорции является фундаментальным. Однако с применением дробных чисел это процедура упрощается до невозможности. Ведь что такое 50% на самом деле? Половина. То есть 1/2 или 0,5 (исходя из начального числа 1). Теперь понятно: чтобы вычислить половину, нужно умножить искомое число или на 1/2, или на 0,5 либо разделить на 2. Такой способ, правда, годится только для чисел, которые делятся без остатка.

В случае возникновения остатка или бесконечных знаков в периоде после запятой типа 0,33333333… лучше использовать дробные выражения наподобие 1/3. Кстати, именно дроби (в некоторых случаях иррациональные) со всей точностью отражают само число, ведь периодические цифры после запятой, сколько ни задавай, все равно целого числа не дадут. А так та же одна треть четко и понятно выражает саму суть.

В тех же рецептах, естественно, треть можно определить, так сказать, на глаз. А вот в химических процессах, особенно связанных с тонкой дозировкой компонентов, скажем, в фармацевтике, такой метод не подойдет. Здесь на глаз полагаться не приходится. Необходимо использовать точные соотношения ингредиентов, даже если один из показателей имеет вид числа с цифрой в периоде или представлен в виде той же иррациональной дроби. Но, как правило, к примеру при взвешивании, такие числа могут ограничиваться после запятой десятитысячными или максимум стотысячными.

Пропорция

Нередки случаи, когда необходимо решить задачи на проценты, используя пропорцию. На самом деле этот метод нахождения результата в значительной мере облегчает задачу учащимся, преподавателям и не только.

Итак, что такое пропорция? Под этим термином понимается равенство двух отношений, которые можно выразить следующим образом: А/_В = С/_D.

В учебниках математики значится такое правило: произведение крайних членов равняется произведению средних. Это выражается следующей формулой: А х D = В х С.

Благодаря этой формулировке, можно вычислить любое число, если три других члена пропорции известны. К примеру, А – неизвестное число. Чтобы его найти, нужно

При решении задач методом пропорции необходимо понимать, от какого числа брать проценты. Бывают случаи, когда доли нужно взять от разных величин. Сравните:

1. После окончания распродажи в магазине стоимость футболки возросла на 25% и составила 200 рублей. Какова была стоимость во время распродажи.

Решение:

В данном случае нужно величина 200 рублей соответствует 125% от первоначальной (распродажной) цены футболки. Тогда, чтобы узнать ее стоимость во время распродажи, нужно (200 х 100) : 125. Получится 160 рублей.

2. На планете Виценция 200 000 жителей: люди и представители гуманоидной расы Наави. Наави составляют 80% от всего населения Виценции. Из людей 40% заняты обслуживанием рудника, остальные добывают тетаниум. Сколько людей добывают тетаниум?

Решение:

В первую очередь нужно найти в численном виде количество людей и количество Наави. Так, 80% от 200 000 будет равняться 160 000. Столько представителей гуманоидной расы проживает на Виценции. Количество людей, соответственно, равняется 40 000. Из них 40%, то есть 16 000, обслуживают рудник. Значит, 24 000 людей занимаются добычей тетаниума.

Условия программы

Еще в феврале 2019 года Владимир Путин призвал разработать доступные финансовые инструменты для поддержки индивидуального жилищного строительства (ИЖС), а условия по ипотечным программам сделать такими же, как для квартир. Для достижения этой цели был разработан пилотный проект по предоставлению льготной ипотеки по ставке 6,1% от «Дом.РФ».

Таким образом, новая программа льготного жилищного кредитования на частные дома была разработана по аналогии с госпрограммой ипотеки под 6,5% для покупки квартир в новостройках. У них очень похожие условия:

1. Заемщиком может быть только гражданин РФ.
2. Кредитный договор должен быть заключен до 01.07.2021.
3. Валюта — только рубли.
4. Жилой дом можно купить в любом российском регионе.
5. Минимальная сумма первоначального взноса по ипотеке — от 20%.
6. Срок кредитования от 3 до 20 лет.
7. Ставка по ипотеке 6,1% на весь срок кредитования.
8. Рефинансировать ипотеку, которая уже есть, по этой программе нельзя — предложение действует только для новых ипотечных договоров.
9. Максимальная сумма ипотеки — 12 млн рублей для Москвы и Санкт-Петербурга, Московской и Ленинградской областей и 6 млн рублей для всех остальных регионов. Взять сумму меньше можно, больше — нельзя.

Налог на доход по вкладам

Налоговый кодекс Российской Федерации предусматривает налогооблажение вкладов в следующих случаях:

• Если процентная ставка по рублевому вкладу превышает значение ключевой ставки ЦБ РФ на момент заключения или пролонгации договора, увеличенной на 5 процентных пунктов.
• Если процентная ставка по валютному вкладу превышает 9%.

Ставка налога составляет 35% для резидентов РФ и 30% для нерезидентов.

При этом налогом облагается не весь доход, полученный от вклада, а только часть, полученная в результате превышения процентной ставки по вкладу пороговой ставки. Для того, чтобы рассчитать налоговую базу (сумму, облагаемую налогом), нужно сначала рассчитать проценты налисленные по номинальной ставке вклада, а затем сделать аналогичный расчет по пороговой ставке. Разница этих сумм и будет являться налоговой базой. Для получения величины налога остается умножить эту сумму на ставку налога.

Наш депозитный калькулятор рассчитает ваш вклад с учетом налогов.

Статьи о кредитах

Вычисление процентов по пропорции

Сейчас мы не будем брать в расчет вычисление процентов с использованием тех же таблиц офисных программ типа Excel, которые делают это в автоматическом режиме при задании соответствующей формулы.

В некоторых случаях используется калькулятор, на котором можно задавать вычисление подобных действий. Но речь сейчас не об этом.

Рассмотрим наиболее распространенные способы вычислений, знакомые нам из школьного курса математики.

Простейшим и самым распространенным способом является решение пропорции.

В данном случае исходное число задается в виде 100 процентов (скажем, некое произвольное число «a»), а его часть (допустим, «b») – в виде неизвестной «x». В математике это выглядит так:

Исходя из правил пропорции, можно вычислить неизвестное число x. Для этого используется так называемый перекрестный метод. Иными словами, нужно умножить b на 100 и разделить на a. Точно такое же правило действует, если в случае составления пропорции поменять b и x местами, когда процент известен, а нужно вычислить часть в числовом выражении.

Как считать проценты в excel?

Если у вас под рукой имеется компьютер или ноутбук с операционной системой Windows, вам не составит большого труда подсчитать процент от необходимой суммы. Приведем для этого простой пример.

Нам необходимо найти 8% от 358.

1. Открываем Excel.
2. Находим свободную строку.
3. Вводим данные.
4. Ставим знак «=» и делаем подсчет.
5. Получаем 28,64.

Аналогично к подсчетам на калькуляторе, вы можете ввести в Excel знак %, и это тоже будет правильно.

Иногда нам необходимо узнать процентный показатель от суммы.

1. К примеру, у нас есть список сотрудников и сумма, на которую они произвели продаж. Помимо этого, известна сумма возвратов. По этим данным мы рассчитываем процент возвратов по товарам.
2. Просчитаем процент для первого показателя в списке — процент возвратов некоего Петрова.
3. Для начала составляем пропорцию, где 100% — это 35682(сумма продаж Петрова). х% — 2023 (сумма возвратов Петрова).
4. Решаем эту пропорцию по формуле, известной нам со школы.
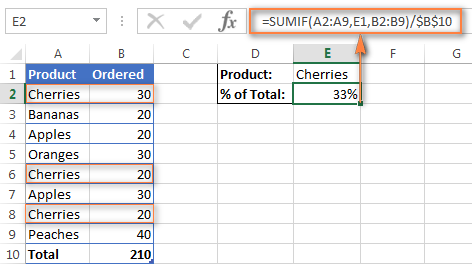
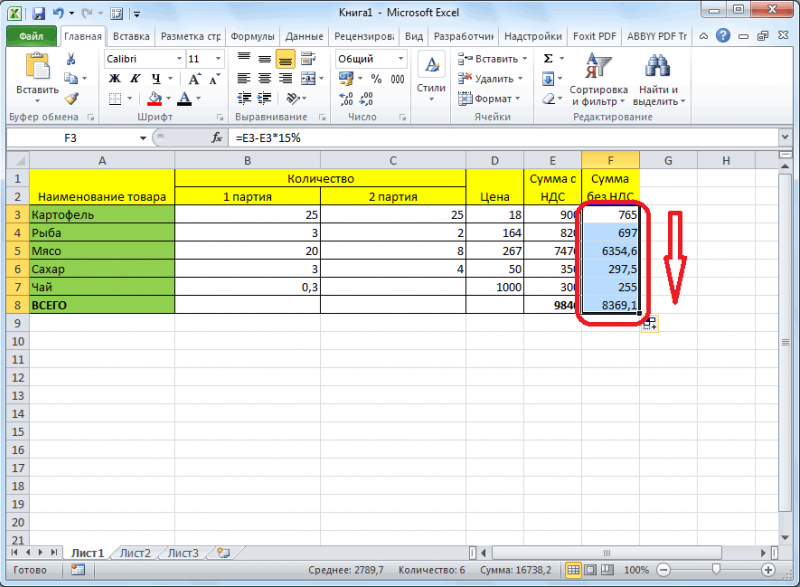
5. Прописываем формулу в ячейке D2 и спускаемся немного вниз =C2*100%/B2.
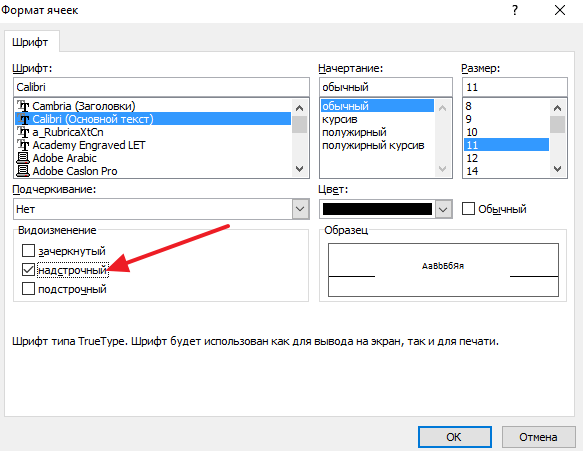
6. К ячейке, в которой высветился результат, применяем формат «Процентный». Выделяем ячейки, правой кнопкой жмем на любой из них и выбираем «Формат». Во вкладке «Число» выбираем «Процентный». Система автоматически пропишет значок %.

7. Применив нашу формулу ко всем данным, получаем результат.