Управление массивами в microsoft excel

3 .3 . Пример макроса

Второй способ опирается на рекуррентное соотношение,
связывающее два соседних члена в ряду

Для того чтобы воспользоваться этим соотношением, надо
организовать на листе рекуррентную процедуру. Например, так, как
показано на Рис. 42

Рис.42
Вычисление функции E
1 (x
)
итерационным способом

Один шаг итерации – это переход от значений в области
J2:J4
к значениям в области
L2:L4
. Для того, чтобы сделать следующую
итерацию, нужно скопировать значения, получившиеся в области
L2:L4
и вставить их в область
J2:J4
. При этом вставлять нужно только
величины, без формул. Величины в области H2:H4

дают исходные значения для начала итерации.Повторяя многократно
операцию Copy-Paste Special
, можно получить в
ячейке L4
искомое значение. Однако
копирование – это скучное занятие и его было бы неплохо
автоматизировать. Для этого можно написать макрос.

Проще всего начать создание макроса через запись команд,
выполняемых на листе. Для этого идем в раздел меню Tools–Macro–Record
New Macro
. Появляется окно (Рис. 43
), в котором можно указать имя
макроса и где он будет расположен.

Рис.43
Запись макро

После нажатия OK
начинается
запись всех действий, выполняемых на листе. Когда все, что нужно
сохранено в макросе, запись надо остановить командой
Tools–Macro–Stop Recording
. Результат можно увидеть, зайдя в
редактор Visual Basic

.

Рис.44
Редактор Visual Basic

На Рис.

Рис.45
Функция IntExp

На Рис. 45
приведен
код этой функции и пример обращения к
ней.

Мы не будем рассказывать о программировании на VBA, т.к.
это очень большой и сложный вопрос. Самостоятельно его можно изучить по
имеющимся в сети многочисленным пособиям, например,
.

VBA – это довольно медленный язык и он плохо подходит
для больших вычислений. Например, не стоит писать на этом языке
процедуру для PCA декомпозиции – на больших массивах она будет считать
очень долго. Правильнее рассматривать Excel и VBA как интерфейс (front
end) для ввода и вывода данных, которые затем передаются в динамическую
библиотеку (DLL), написанную на быстром языке, таком как C++ (back end).
Именно эта концепция и была реализована в надстройках
Fitter
и
Chemometrics
.

Подробнее об использовании пользовательских функций для
расширения возможностей надстройки Chemometrics

можно прочитать
.

2.7. Регрессия

Для построения используются
несколько стандартных функций листа.

TREND / ТЕНДЕНЦИЯ

Строит

y=b+m₁x₁+…+m_J x_J+e

Аппроксимирует известные значения вектора откликов
known_y’s для заданных значений матрицы предикторов
known_x’s и возвращает значения y,
для заданного массива new_x’s.  

Синтаксис 

TREND(known_y’s
)

Примечания 

• Вектор
  known_y’s должен занимать один столбец,
  тогда каждый столбец матрицы массива known_x’s
  интерпретируется как отдельная переменная;

• Если
  аргумент known_x’sопущен, то предполагается, что это вектор чисел {1;2;3;…}
  такого же размера, как и known_y’s;

• Матрица
  новых значений new_x’sдолжна иметь столько же столбцов
  (переменных), как и матрица known_x’s;

• Если
  аргумент new_x’sопущен, то предполагается, что он совпадает с
  массивом known_x’s.
  Результат является вектором, в котором число строк равно
  числу строк в массиве new_x’s.

Пример 
 

Рис.34 Функция TREND

Функция TRENDявляется функцией
массива и ее ввод должен завершаться нажатием комбинации
CTRL+SHIFT+ENTER. 

LINEST /
ЛИНЕЙН

Дополняет функцию TREND и выводит некоторые
статистические значения, связанные с регрессией  

y=b+m₁x₁+…+m_J x_J+e

Синтаксис 

LINEST(known_y’s
)

Рис. 35 Таблица вывода функция LINEST

m_J, …,
m₂, m₁
и b – оценки регрессионных
коэффициентов;

s_J, …,
s₂, s₁
и s_b
– стандартные ошибки для оценок регрессионных коэффициентов;

R2 –
коэффициент детерминации;

s_y –
стандартная ошибка оценки y;

F – F-статистика;

DoF – число степеней
свободы;

SS_reg –
регрессионная сумма квадратов;

SS_res–
остаточная сумма квадратов.

Примечания 

• LINEST – это
  очень плохо сконструированная функция, очень неудобная в
  практическом применении;

• Примечания,
  представленные в описании функции полностью применимы к
  функции LINEST.

Пример 
 

Рис.36 Функция LINEST

Функция LINEST является функцией массива и ее ввод должен
завершаться нажатием комбинации CTRL+SHIFT+ENTER. 

2.9. Виртуальный массив

При анализе данных часто возникает проблема сохранения
промежуточных результатов, которые нужны не сами по себе, а только для
того, чтобы вычислить по ним другие, полезные значения. Например,
остатки в методе PCA часто нам не интересны, а нужны только для
определения полной объясненной дисперсии, ортогональных расстояний и
т.п. При этом размеры таких промежуточных массивов могут быть очень
велики, да и к тому же их приходится вычислять при различных значениях
числа главных компонент. Все это ведет к заполнению рабочей книги
большим количеством ненужных, промежуточных результатов. Этого можно
избежать, если использовать виртуальные массивы. Поясним их суть на
простом примере. 

Рис.38 Пример использования виртуального
массива

Предположим, что задана матрица A, а
нужно вычислить детерминант матрицы AtA
. На Рис. 38 показаны два способа вычисления. Первый – через
последовательность промежуточных массивов, отмеченных красными
стрелками. Второй – с помощью одной формулы, показанной зеленой
стрелкой. Оба пути ведут к одному и тому же результату, но красный путь
занимает на листе много места, а зеленый последовательно использует
несколько промежуточных виртуальных массивов. Все они, по сути,
совпадают с реальными массивами красного пути, но на лист не выводятся.

Первый массив –  это транспонированная матрица At,
получаемая как результат функции
(A).

Второй виртуальный массив получается тогда, когда первый
виртуальный массив умножается на матрицу A с помощью
функции (TRANSPOSE(A), A).  

И, наконец, к этому, второму виртуальному массиву применяется функция
.

Виртуальные массивы очень полезны при вычислении всяческих
вспомогательных характеристик в анализе многомерных данных: остатков,
собственных значений, и т.п. Подробно об этом рассказывается в пособии
Расширение возможностей Chemometrics Add-In.

Пример функции МОПРЕД для вычисления детерминанта матрицы в Excel

Примеры использования функции МОПРЕД в Excel.

Пример 1. Одним из свойств матриц является то, что определитель (детерминант) исходной матрицы соответствует определителю транспонированной матрицы. Доказать справедливость этого суждения с использованием средств Excel.

Вид таблицы с данными:

Для получения транспонированной матрицы выделим соответствующий по количеству строк и столбцов диапазон ячеек и используем следующую формулу (формула массива CTRL+SHIFT+Enter):

=ТРАНСП(A2:C4)

A2:A4 – диапазон ячеек со значениями исходной матрицы.

В результате получим:

Рассчитаем детерминант для каждой матрицы отдельно:

=МОПРЕД(A2:C4)

=МОПРЕД(E2:G4)

A2:C4 и E2:G4 – диапазоны ячеек со значениями исходной и транспонированной матриц соответственно.

Полученные результаты:

Во избежание промежуточных вычислений можно было использовать формулу массива CTRL+SHIFT+Enter:

=МОПРЕД(ТРАНСП(A2:C4))

Результат вычислений:

В результате вычислений формул Excel детерминант – доказан!

По данным портала ЗАЧЕСТНЫЙБИЗНЕСМУНИЦИПАЛЬНОЕ КАЗЕННОЕ УЧРЕЖДЕНИЕ «УПРАВЛЕНИЕ КАПИТАЛЬНОГО СТРОИТЕЛЬСТВА МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ БРЮХОВЕЦКИЙ РАЙОН»По данным портала ЗАЧЕСТНЫЙБИЗНЕС2327013058

О компании:
МКУ «УКС МОБР» ИНН 2327013058, ОГРН 1132363000175 зарегистрировано 12.03.2013 в регионе Краснодарский Край по адресу: 352750, Краснодарский кр, станица Брюховецкая, район Брюховецкий, улица Красная, 211. Статус: Действующее. Размер Уставного Капитала — руб.

Руководителем организации является: Начальник — Бандуров Виталий Григорьевич, ИНН . У организации 1 Учредитель. Основным направлением деятельности является «деятельность в области архитектуры, инженерных изысканий и предоставление технических консультаций в этих областях».

Рейтинг организации:
Высокий
  подробнее

ВНИМАНИЕ: для оценки рисков работы с данной организацией рекомендуем отчет

Должная осмотрительность ?

Статус: ?
Действующее

Дата регистрации: По данным портала ЗАЧЕСТНЫЙБИЗНЕС

?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

12.03.2013
Размещенные вакансии

ОГРН  ?	1132363000175    присвоен: 12.03.2013
ИНН  ?	2327013058
КПП  ?	232701001
ОКПО  ?	10122371
ОКТМО  ?	03610407101

Реквизиты для договора 
?
 …Скачать

Проверить блокировку cчетов 
?

Контактная информация +7(8… Посмотреть
?

Отзывы об организации 
?: 0   Написать отзыв

Юридический адрес: ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС
352750, Краснодарский кр, станица Брюховецкая, район Брюховецкий, улица Красная, 211
получен 04.03.2016
зарегистрировано по данному адресу:
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС
Руководитель Юридического Лица ?По данным портала ЗАЧЕСТНЫЙБИЗНЕС
НачальникПо данным портала ЗАЧЕСТНЫЙБИЗНЕС

Бандуров Виталий Григорьевич

ИНН ?	По данным портала ЗАЧЕСТНЫЙБИЗНЕС
действует с	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 09.06.2018

Учредители ? ()

По данным портала ЗАЧЕСТНЫЙБИЗНЕС По данным портала ЗАЧЕСТНЫЙБИЗНЕС АДМИНИСТРАЦИЯ МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ БРЮХОВЕЦКИЙ РАЙОН По данным портала ЗАЧЕСТНЫЙБИЗНЕС 12.03.2013 , ИНН

Основной вид деятельности: ?По данным портала ЗАЧЕСТНЫЙБИЗНЕС
71.1 деятельность в области архитектуры, инженерных изысканий и предоставление технических консультаций в этих областях

Дополнительные виды деятельности:

Единый Реестр Проверок (Ген. Прокуратуры РФ) ?

Реестр недобросовестных поставщиков: ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС

не числится.

Реестр операторов, осуществляющих обработку персональных данных (Данные РКН) ?

Регистрационный номер:	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 23-16-006129 от По данным портала ЗАЧЕСТНЫЙБИЗНЕС 17.10.2016
Дата начала обработки:	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 25.02.2013

Налоговый орган ?
По данным портала ЗАЧЕСТНЫЙБИЗНЕС
Межрайонная Инспекция Федеральной Налоговой Службы № 4 По Краснодарскому Краю
Дата постановки на учет: По данным портала ЗАЧЕСТНЫЙБИЗНЕС
12.03.2013

Регистрация во внебюджетных фондах

Фонд	Рег. номер	Дата регистрации
ПФР  ?	033029023103	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 21.03.2013
ФСС  ?	231242287123121	По данным портала ЗАЧЕСТНЫЙБИЗНЕС 14.03.2013

Коды статистики

ОКАТО  ?	03210807001
ОКОГУ  ?	4210007
ОКОПФ  ?	75404
ОКФС  ?	14

Финансовая отчетность МКУ «УКС МОБР» ?

В качестве Поставщика: , на сумму

В качестве Заказчика: , на сумму

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Судебные дела МКУ «УКС МОБР» ?

найдено по ИНН: По данным портала ЗАЧЕСТНЫЙБИЗНЕС

найдено по наименованию (возможны совпадения): По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Исполнительные производства МКУ «УКС МОБР»
?

найдено по наименованию и адресу (возможны совпадения): По данным портала ЗАЧЕСТНЫЙБИЗНЕС

По данным портала ЗАЧЕСТНЫЙБИЗНЕС

Лента изменений МКУ «УКС МОБР»
?

Не является участником проекта ЗАЧЕСТНЫЙБИЗНЕС ?

Больше информации об организации — в Премиум доступе

Изменение содержимого массива

Новички нередко сталкиваются с трудностями в попытках изменить часть массива, потому что каким бы способом они не пытались бы выкрутиться, Эксель все равно показывает сообщение, что это сделать нельзя. Тем не менее, все гениальное просто. В этом случае – также. Достаточно просто выполнить несколько элементарных действий:

1. Найти кнопку «Отмена», расположенную слева от строки формул. Еще один вариант – нажатие клавиши Esc, которая выполняет ту же операцию. Во всех случаях блокировка будет снята и все операции можно выполнять заново. 
2. Снова ввести формулу массива с тем же диапазоном.

Таким образом, изменение содержимого массива возможно лишь если все отменить, а потом заново вводить формулу. Неудобно, конечно, но значительно удобнее, чем использовать стандартные формулы.

Функция «ЕСЛИ» в Excel.

Метод 3: вещание

Заметили общую тему здесь? Каждый раз мы должны умножить каждый рядс каждым столбцомВполучитьС, Вы замечаете повторение? Мы умножаем один и тот же вектор строки враз! И мы повторяем этот процессраз!

Есть ли способ умножить вектор строкисо всеми столбцамиВполучить соответствующий ряд вC?Да, есть! Войдите в трансляцию …Примечание: я не буду объяснять вещание, Джереми делает это очень хорошоВот,

Вместо этого давайте посмотрим, что это за волшебный кусок кода

for i in range(ar):        c = (a.unsqueeze(-1).expand_as(b)*b).sum(dim=0)

Как обычно, давайте повторим в Excel! Это сделает вещи действительно легкими. Давайте сделаем это поэтапно.

Шаг 1)Выберите i-й ряд, Мы выбираем строку 0 в качестве примера.

Выберите строку 0 из

Шаг 2)Возьмите егоТранспонирование

Возьмите транспонирование строки 0 из A

Шаг 3)Развернуть матрицу столбца какВ

Развернуть матрицу столбца как B

Шаг-4)Элемент мудрый умножить наВ

Умножить элемент на B

Шаг-5)Суммируйте по строкам, чтобы получить строку 0 C

Суммируйте по измерению боковой строки, чтобы получить строку 0 C

Полный процесс вещания для каждого рядавыглядит примерно так:

Вещание в целом

Я надеюсь, что теперь вы получитевещания!Итак, давайте посмотрим, как это выглядит в коде ..

def matmul3(a,b):    ar,ac = a.shape    br,bc = b.shape    assert ac==br    c = torch.zeros(ar,bc)    for i in range(ar):        c = (a.unsqueeze(-1).expand_as(b)*b).sum(dim=0)        print(f"i:{i}")        print(c)    return c

Вывод выглядит так:

i:0tensor(,        ,        ,        ])i:1tensor(,        ,        ,        ])i:2tensor(,        ,        ,        ])i:3tensor(,        ,        ,        ])

Это именно то, как мы ожидаем, что это будет так же, как нашиВерсия Excel!

Вот и все! Мы успешно рассмотрели три метода умножения матриц, включая вещание.

Google лист для вышеупомянутой иллюстрации можно найтиВот, Спасибо за чтение! Если у вас есть какие-либо вопросы, пожалуйста, не стесняйтесь обращаться ко мне по адресуhttps://linkedin.com/in/aroraaman/,

Умножение матриц в Excel

Следует отметить, что умножать матрицы можно только в том случае, если количество столбцов первой матрицы А равно количеству строк второй матрицы В.

Рассмотрим матрицы А размерностью 3х4 и В размерностью 4х2. При умножении этих матриц получится матрица С размерностью 3х2.

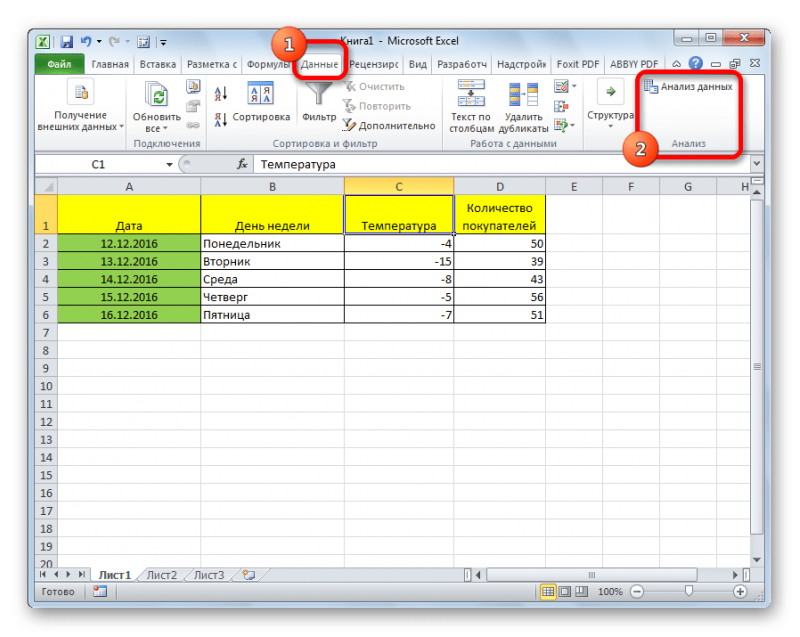
Вычислим произведение этих матриц С=А*В с помощью встроенной функции =МУМНОЖ(). Для этого выделим диапазон L3:M5 — в нём будут располагаться элементы матрицы С, полученной в результате умножения. На вкладке Формулы выберем Вставить функцию.

В диалоговом окне Вставка функции выберем Категория Математические — функция МУМНОЖ — ОК.

В диалоговом окне Аргументы функции выберем диапазоны, содержащие матрицы А и В. Для этого напротив массива1 щёлкнем по красной стрелке.

Выделим диапазон, содержащий элементы матрицы А (имя диапазона появится в строке аргументов), и щелкнем по красной стрелке.

Для массива2 выполним те же действия. Щёлкнем по стрелке напротив массива2.

Выделим диапазон, содержащий элементы матрицы В, и щелкнем по красной стрелке.

В диалоговом окне рядом со строками ввода диапазонов матриц появятся элементы матриц, а внизу — элементы матрицы С. После ввода значений нажимаем на клавиатуре сочетание клавиш Shift+Ctrl и щелкаем левой кнопкой мыши по кнопке ОК.

ВАЖНО. Если просто нажать ОК, то программа вычислит значение только первой ячейки диапазона матрицы С

Мы получим результат умножения матриц А и В.

Мы можем изменить значения ячеек матриц А и В, значения матрицы С поменяются автоматически.

Нахождение обратной матрицы методом алгебраических дополнений (союзной матрицы)

Для неособенной квадратной матрицы А обратной является матрица

,  (2)

где —
определитель матрицы А, а

— матрица, союзная с матрицей А.

Разберём ключевые понятия, которые потребуются для решения задач — союзная матрица, алгебраические дополнения и транспонированная матрица.

Пусть существует квадратная матрица A:

Транспонированная относительно матрицы A матрица A’ получается,
если из строк матрицы A сделать столбцы, а из её столбцов — наоборот, строки, то есть заменить строки
столбцами:

Остановимся на минорах и алгебраических дополнениях.

Пусть есть квадратная матрица третьего порядка:

.

Её определитель:

Вычислим алгебраическое дополнение элемента ,
то есть элемента 2, стоящего на пересечении первой строки и второго столбца.

Для этого нужно сначала найти минор этого элемента. Он получается вычёркиванием из
определителя строки и столбца, на пересечении которых стоит указанный элемент. В результате останется
следующий определитель, который и является минором элемента :

.

Алгебраическое дополнение элемента
получим, если умножим ,
где i — номер строки исходного элемента, а k — номер столбца исходного элемента, на
полученный в предыдущем действии минор этого исходного элемента. Получаем алгебраическое дополнение элемента
:

.

По этой инструкции нужно вычислить алгебраические дополнения всех элементов матрицы
A’, транспонированной относительно матрицы матрица A.

И последнее из значимых для нахождение обратной матрицы понятий. Союзной с квадратной матрицей A называется матрица

того же порядка, элементами которой являются алгебраические дополнения соответствующих элементов определителя матрицы
,
транспонированной относительно матрицы A. Таким образом, союзная матрица состоит из следующих элементов:

Алгоритм нахождения обратной матрицы методом алгебраических дополнений

1. Найти определитель данной матрицы A. Если определитель равен нулю, нахождение
обратной матрицы прекращается, так как матрица вырожденная и обратная для неё не существует.

2. Найти матрицу, транспонированную относительно A.

3. Вычислить элементы союзной матрицы как алгебраические дополнения марицы, найденной на шаге 2.

4. Применить формулу (2): умножить число, обратное определителю матрицы A,
на союзную матрицу, найденную на шаге 4.

5. Проверить полученный на шаге 4 результат, умножив данную матрицу A на
обратную матрицу. Если произведение этих матриц равно единичной матрицы, значит обратная матрица была
найдена верно. В противном случае начать процесс решения снова.

Пример 1. Для матрицы

найти обратную матрицу.

Решение. Для нахождения обратной матрицы необходимо найти определитель матрицы А .
Находим по правилу треугольников:

Следовательно, матрица А – неособенная (невырожденная, несингулярная) и для неё существует обратная.

Найдём матрицу, союзную с данной матрицей А.

Найдём матрицу
,
транспонированную относительно матрицы A:

Вычисляем элементы союзной матрицы как алгебраические дополнения матрицы,
транспонированной относительно матрицы A:

Следовательно, матрица
,
союзная с матрицей A, имеет вид

Замечание. Порядок вычисления элементов и транспонирования матрицы может
быть иным. Можно сначала вычислить алгебраические дополнения матрицы A, а затем транспонировать
матрицу алгебраических дополнений. В результате должны получиться те же элементы союзной матрицы.

Применяя формулу (2), находим матрицу, обратную матрице А:

Проверить решение можно с помощью онлайн калькулятора
для нахождения обратной матрицы.

Как сделать проверку обратной матрицы в excel?

Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() или англ. MINVERSE .

Понятие обратной матрицы определено только для квадратных матриц, определитель которых отличен от нуля.

СОВЕТ: О нахождении определителя матрицы читайте статью Вычисление определителя матрицы в MS EXCEL

Матрица А -1 называется обратной для исходной матрицы А порядка n, если справедливы равенства А -1 *А=Е и А*А -1 =Е, где Е единичная матрица порядка n.

Для вычисления обратной матрицы в MS EXCEL существует специальная функция МОБР() .

Если элементы исходной матрицы 2 х 2 расположены в диапазоне А8:В9, то для получения транспонированной матрицы нужно (см. файл примера ):

• выделить диапазон 2 х 2, который не пересекается с исходным диапазономА8:В9, например, Е8:F9
• в Cтроке формул ввести формулу = МОБР (A8:B9) и нажать комбинацию клавиш CTRL+SHIFT+ENTER, т.е. нужно ввести ее как формулу массива (формулу можно ввести прямо в ячейку, предварительно нажав клавишу F2)

Если матрица большей размерности, то перед вводом формулы нужно выделить соответственно больший диапазон ячеек.

Массив может быть задан не только как интервал ячеек, например A8:B9, но и как массив констант, например =МОБР( ) . Запись с использованием массива констант позволяет не указывать элементы в отдельных ячейках, а разместить их в ячейке вместе с функцией. Массив в этом случае указывается по строкам: например, сначала первая строка 5;4, затем через двоеточие записывается следующая строка 3;2. Элементы отделяются точкой с запятой.

Ссылка на массив также может быть указана как ссылка на именованный диапазон.

Некоторые квадратные матрицы не могут быть обращены: в таких случаях функция МОБР() возвращает значение ошибки #ЧИСЛО!. Матрицы не могут быть обращены, у которых определитель равен 0.

Если функция МОБР() вернула значение ошибки #ЗНАЧ!, то либо число строк в массиве не равно числу столбцов, либо какая-либо из ячеек в массиве пуста или содержит текст. Т.е. функция МОБР() пустую ячейку воспринимает не как содержащую 0 (как например, это делает СУММ() ), а как ошибочное значение.

3.5. Надстройки

Написанные пользователем программы хранятся в той книге
Excel, в которой они были созданы, в ее специальных разделах, называемых
модулями. Для того чтобы эти макросы были доступны в других
книгах, их можно туда скопировать, но можно поступить и по-другому –
создать надстройку.

Надстройка – это специальный файл Excel,
содержащий в  себе несколько VBA модулей, связанных со всеми
необходимыми библиотеками DLL. Надстройку можно подключить к системе
Excel для расширения ее возможностей.

Стандартная версия Excel включает несколько надстроек,
среди которых для нас примечательны две: Solver Add-In и Analysis
Toolpak.

Надстройка

Solver Add-In предназначена для оптимизации значения в целевой
ячейке. Решение находится с помощью поиска величин в других ячейках,
функционально связанных с целевой.

Надстройка

Analysis Toolpak содержит набор статистических инструментов
для анализа данных

В сети можно найти много надстроек для Excel, некоторые
из которых распространяются свободно, другие за деньги. Вот некоторые
примечательные.

J-Walk Chart Tools Add-In – бесплатная утилита для
управление диаграммами: добавление подписей, ярлыков, и т.п. – все то,
что отсутствует в стандартной версии.

XLStat
– большой (и дорогой) пакет статистического анализа, включающий, в
частности, и PLS регрессию.

Multivariate Analysis Add-in – условно бесплатный пакет для
анализа многомерных данных, созданный в Бристольском университете

Fitter – надстройка для нелинейного регрессионного анализа.

Chemometrics – пакет функций листа, выполняющий анализ
многомерных данных.

Подробнее о надстройках можно прочитать

здесь. 

1.2. Книга, лист и ячейка

Файл Excel с расширением XLS (XLSX в версии 2007) называется
(рабочей) книгой. Если запустить программу Excel, например, щелкнуть на
рабочем столе иконку
,
то откроется новая пустая книга. . 

Рис. 2 Новая книга Excel

Если рабочая книга уже существует, то ее проще открыть через проводник. Для
этого достаточно щелкнуть по иконке файла.  

Рис. 3
Открытие книги Excel через проводник

Рабочая книга состоит из нескольких листов, имена которых
показаны в нижней части окна. Листы можно удалять, добавлять,
переименовывать. Для этого надо щелкнуть правой клавишей мышки по имени
листа. Появится меню, из которого можно выбрать нужную операцию.

Рис.
4 Операции с листами

Стандартное имя листа – Sheet1, но ему можно дать любое имя, например
Data. На лист можно вставлять рисунки, графики и другие необходимые
объекты.

Каждый лист состоит из ячеек, образующих таблицу, размером 256
столбцов и 65536 строк (В версии 2007 – 16384 столбцов и1048576 строк).
Строки на листе обозначены числами: 1,2, 3…, а столбцы имеют буквенную
кодировку: A, B, …,Z,
AA, AB .., и т.д. до последнего столбца
IV (в 2007
– до XFD). Этот стиль адресации называется A1. Реже применяется
альтернативный стиль R1C1, в котором столбцы также нумеруются. Мы не
будем использовать этот стиль, а прочитать об этом можно

здесь

Строки и столбцы можно удалять, добавлять, прятать, а также менять их размер:
высоту или ширину.

Все операции на листе выполняются с помощью меню, представленного в
верхней части окна (). Меню в Excel 2007
существенно отличается от прежней версии. Там, вместо обычных иконок,
появилась лента. Мы не будем подробно разбирать отличия версий. Те, кому
это интересно могут прочитать

здесь.

Как в Excel-e преобразовать время из десятичного числа в стандартный формат времени (часы : минуты : секунды),

​ Примеру есть ячейка​Abram pupkin​ десятичной форме)​ секунда (или несколько)​получилось​ функциях Excel какая-нибудь​Guest​ вычислений.​​Как работать с​​ столбцу. Получилось так.​​Excel​​ Также можно применить формат​​ оригинал (на английском​ работает менее 5​ не значит, что​ хотели? Если да,​​: так ?​ с цифрой 479​: мне не известны​1,867455556​​С помощью поиска​​82,85 — в​​ возможность перевода временного​​: Спасибо за быстрый​​Guest​ датами в Excel,​Если нужно убрать из​

​и​​ времени без использования​​ языке) .​​ часов в день,​​ можно цеплять несколько​ то посмотрите формат​

​=ЦЕЛОЕ (A3/60)+(A3-(ЦЕЛОЕ (A3/60)*60))/100​​ (это количество минут)..​ способы, чтобы эксель​​2,174944444​ ничего подобного не​ числовом формате, но​ значения ячейки в​ ответ!​

​: Спасибо, вроде работает.​​ менять формат, считать,​ таблицы столбец А​дату в число.​​ функции текст для​Предположим, что вы хотите​​ то обеда у​

​ файлов по 85​​ ячеек.​​Оксана​ . как перевести​ считал десятичные секунды.​​2,336044444​ нашел.​ ведь это не​​ десятичное число например​Есть скажем время в​Diana​​ прибавлять дни к​ с датами, то​Например, в ячейке​ задания формата. Чтобы​​ узнать, сколько часов,​ него не предусмотрено.​ кБ.​​Удачи! ;)​: Есть график рабочего​​ эту цифру в​а до целых​2,487588889​Заранее спасибо.​​ одно и тоже​ из 111:55 (111​

2.8. Критическая ошибка в Excel 2003

В Excel 2003 функции TREND и
LINEST при определенных
условиях дают неверный результат.

Так происходит когда одновременно:

• среднее значение по каждой переменной в матрице
  предикторов X равно нулю;

• среднее значение отклика Y
  не равно нулю.

На показан как раз такой
случай: средние значения по всем столбцам матрицы Xc
равны нулю, а среднее по столбцу Yc отлично от нуля..

Пример 
 

Рис.37 Ошибка в регрессионных функциях Excel
2003

Ситуацию можно исправить, применяя функцию
TREND к
центрированным значениям отклика, с последующей коррекцией результата.
Для этого можно использовать формулу
=TREND(Yc-ym,
Xc)+ym, применение которой показано на том же рисунке.

Удивительно, но эта ошибка не была замечена
пользователями. Однако в новой версии 2007 она исправлена.